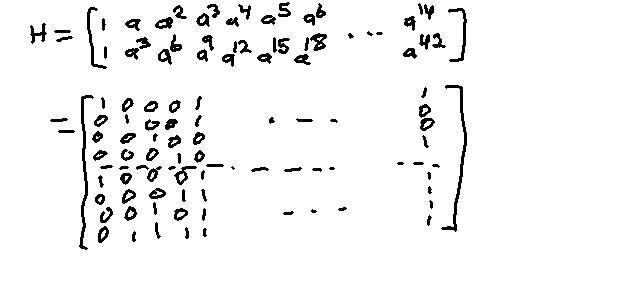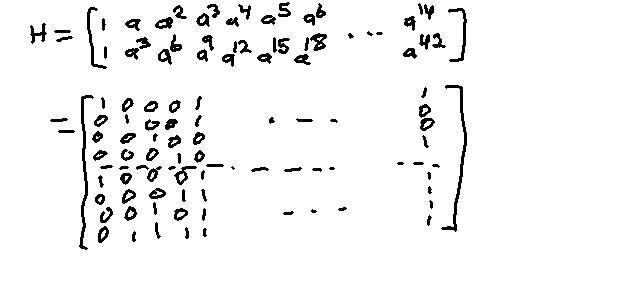Chapter 6 - Binary BCH Codes

Properties

• For any m >= 3, t < 2^m-1
  • Block Length: n = 2^m-1
  • # parity check bits: n - k < m*t
  • Min distance: d_min >= 2t + 1
  • Corrects up to t errors; called a "t error correcting BCH Code"

Generator Polynomial

• The generator g(X) is the lowest degree polynomial in GF(2^m) which has a,a²,a³,a⁴,...a^2t as its roots
• g(X) = LCM{Q₁(X),Q₃(X),...Q_2^t-1(X)} (Least Common Multiple)
  • Q_i(X) is the min polynomial for aⁱ

Parity Check Matrix

• Format:

  

• Example: Parity check matrix for n = 2⁴ - 1, t = 2, p(X) = 1+X+X⁴

  

Alternative Syndrome Calculation

• As usual, S=(S₁,S₂,S₃...S_2t) = r*H^t
• However, they can also be computed via the following:
  • S_i = b_i(X), where
    • b_i(X) is the remainder of r(X) / min_poly(aⁱ)
      • See chapter two for a refresher of calculting the min polynomial
    • aⁱ is the power representation of the i^th codeword in the BCH code

Decoding BCH Codes

1. Compute syndrome S = (S1,S2,S3,...S2t) from received r
2. Determine Error Polynomial σ(X) from S
3. Find error location numbers β1,β2,...βv, by finding the roots of σ(X)

Error location polynomial σ(X)

• σ(X) = σ₀ + σ₁X + σ₂X² ... σ_vX^v, where v is the number of errors
• Needs to be calculated; hardest step of decoding. One way to calculate it is Berlkamp Iterative Algorithm

Berlekamp Iterative Algorithm

1. Find the minimum degree polynomial σ^μ=1(X) satisfying Newton's μ^th identity (identities below) for the first iteration, μ = 1
   • S₁ + σ₁ = 0
   • S₂ + σ₁S₁ + 2σ₂ = 0
   • S₃ + σ₁S₂ + σ₂S₁+ 3σ₃ = 0
   • ...
   • S_μ + σ₁S_μ-1 + ... + σ_μ-1S₁ + μσ_μ = 0
   • For binary, iσ_i = σ_i if i is odd, else 0 if i is even
2. Test if σ^μ=1(X) also satisfies the second identity S₂ + σ₁S₁ + 2σ₂ = 0
   • If true, then set σ^μ=2(X) equal to σ^μ=1(X)
   • Else add a correction (from a previously calculated σ(X)) to σ^μ=2(X) so that the second identity is satisfied
     • σ^μ+1(X) = σ^μ(X) + d_μ d_p^-1X^μ-pσ^p(X)
       • d_μ = S_μ+1 + σ₁ ^μS_μ + σ₂^μS_μ-1 + ... σ_lμ^μS_μ+1-lμ
       • d is called the discrepancy
       • p is the iteration number where d_μ is not 0 and p - l_p has the largest value (l_p is the degree of σ^p(X))
3. Repeat until we have σ^μ=2t(X); this is our error location polynomial σ(X)
4. Keep track using a table, which 2 previous starting entries:

   μ	σμ(X)	dμ	lμ	μ-lμ
   -1	1	1	0	-1
   0	1	S1	0	0
   1
   2
   ...
   2t

BCH Decoding Example

• (15,5) triple-error-correcting (t=3) BCH code from example 6.1, generator p(X) = 1 + X + X⁴
• v = (0000000000000000)
• r = (0001010000000100) = X³ + X⁵ + X¹²
• Calculate Syndrome: Calculate minimal polynomials
  • φ(a) = φ(a²) = φ(a⁴) = φ(a⁸) = 1 + X + X⁴
  • φ(a³) = φ(a⁶) = φ(a¹²) = (X+a³)*(X+(a³)²)*(X+(a³)⁴)* (X+(a³)⁸)
    • = (X+a³)*(X+a⁶)*(X+a¹²)*(X+a²⁴)
    • = (X+a³)*(X+a⁶)*(X+a¹²)*(X+a⁹) // 24 MOD 15 == 9
    • = (X² + (a⁶ + a³)X + a⁹) * (X² + (a⁹ + a¹²)X + a⁶)
    • = (X² + (a² + a³ + a³)X + a⁹) * (X² + (a + a³ + 1 + a + a² + a³)X + a⁶) // substitute from table 2.8 (polynomial representations)
    • = (X² + a²X + a⁹) * (X² + a⁸X + a⁶)
    • = X⁴ + a⁸X³ + a⁶X² + a¹⁰X² + a²X³ + a⁸X + a⁹X²+ a¹⁷X + a¹⁵
    • = X⁴ + (a⁸ + a²)X³ + (a⁶ + a¹⁰ + a⁹)X² + (a⁸ + a¹⁷)X + 1
    • = X⁴ + (1 + a² + a²)X³ + (a² + a³ + 1 + a + a² + a + a³)X² + (1 + a² + a²)X + 1
    • = X⁴ + (1)X³ + (1)X² + (1)X + 1
    • = X⁴ + X³ + X² + X + 1
  • φ(a⁵) = φ(a¹⁰) = (X+a⁵)*(X+(a⁵)²) (stop here since a^{20 MOD 15} = a⁵)
    • (X + a⁵)*(X + a¹⁰)
    • = X² + (a¹⁰ + a⁵)X + a⁵a¹⁰
    • = X² + (1 + a + a² + a + a²)X + a¹⁵
    • = X² + X + 1
• Syndrome will be of length 6 (2t, t=3 since triple error correcting), so need min polys up to a⁶
• Calculate syndrome: Divide r by min polynomials to get remainders
  • (X³ + X⁵ + X¹²) / (1 + X + X⁴) = X⁸ + X⁵ + X⁴ + X² + X + 1
    • remainder b₁(X) = b₂(X) = b₄(X) = 1
  • (X³ + X⁵ + X¹²) / (1 + X + X² + X³ + X⁴) = X⁸ + X⁷ + X³ + X² + X + 1
    • remainder b₃(X) = b₆(X) = X³ + X² + 1
  • (X³ + X⁵ + X¹²) / (1 + X + X²) = X¹⁰ + X⁹ + X⁷ + X⁶ + X⁴ + X²
    • remainder b₅(X) = X²
• Calculate Syndromes: plug a...a⁶ into remainders
  • b₁(a) = b₂(a²) = b₄(a⁴) = 1 = S1,S2,S4
  • b₃(a³) = S3
    • = 1 + (a³)² + (a³)³
    • = 1 + a⁶ + a⁹
    • = 1 + a² + a³ + a + a³
    • = 1 + a + a²
    • = a¹⁰
  • b₆(a⁶) = S6
    • = 1 + (a⁶)² + (a⁶)³
    • = 1 + a¹² + a¹⁸
    • = 1 + 1 + a + a² + a³ + a³
    • = a + a²
    • = a⁵
  • b₅(a⁵) = S5
    • = (a⁵)²
    • = a¹⁰
• Berlekamp Iterative Algorithm
  • Start with base table as described earlier

    μ	σμ(X)	dμ	lμ	μ-lμ
    -1	1	1	0	-1
    0	1	S1=1	0	0
    1
    2
    ...
    2t

  • Next, calculate using μ = 0
    • d_μ=0 = 1, so need to pick prev. row p
    • p = -1 since only previous row (meets criteria that d_p =/= 0 with highest μ - l_μ val)
    • Calculate σ^μ+1(X) = σ^μ(X) + d_μd_p^-1X^μ-p σ^p(X)
      • = σ⁰(X) + 1(1^-1)X^0-(-1) σ^-1(X)
      • = 1 + 1(1)X¹(1)
      • = 1 + X
    • Calculate l_μ+1=1=max(l_μ,l_p+μ-p)
      • = max(0,0+0-(-1))
      • = 1
    • Calculate d_μ+1=1 = S_μ+2 + σ₁^μ+1S_μ+1 ... + σ_lμ+1^μ+1 S_μ+2-lμ+1
      • Calculate the lowest S_i used to figure out when to stop
        • μ+2-l_μ+1 = 0+2-1=1, so the last S is S₁ = S_μ+1 (since μ=0)
      • S_μ+2 + σ₁^μ+1S_μ+1
        • = 1 + 1(1)
        • = 0
  • Fill in the next row μ+1 = 1 with the calculated values

    μ	σμ(X)	dμ	lμ	μ-lμ
    -1	1	1	0	-1
    0	1	S1=1	0	0
    1	1 + X	0	1	0
    2
    ...
    2t

  • Next, calculate using μ = 1
    • d_μ=1 = 0, so σ^μ(X) matches our next Newton's identity criteria
    • Set σ^μ+1(X) = σ^μ(X) = 1 + X
    • Set l_μ+1 = l_μ = 1
    • Calculate d_μ+1=1 = S_μ+2 + σ₁^μ+1S_μ+1 ... + σ_lμ+1^μ+1 S_μ+2-lμ+1
      • Calculate the lowest S_i used to figure out when to stop
        • μ+2-l_μ+1 = 1+2-1=2, so the last S is S₂ = S_μ+1 (since μ=1)
      • S_μ+2 + σ₁^μ+1S_μ+1
        • = a¹⁰ + 1(1)
        • = 1 + a + a² + 1
        • = a + a²
        • = a⁵
  • Fill in the next row μ+1 = 2 with the calculated values

    μ	σμ(X)	dμ	lμ	μ-lμ
    -1	1	1	0	-1
    0	1	S1=1	0	0
    1	1 + X	0	1	0
    2	1 + X	a5	1	1
    ...
    2t

  • Next, calculate using μ = 2
    • d_μ=2 = a⁵, so need to pick previous row p
      • p = 0 since non-zero d_μ with highest μ-l_μ
    • Calculate σ^μ+1(X) = σ^μ(X) + d_μd_p^-1X^μ-p σ^p(X)
      • = σ²(X) + a⁵(1^-1)X² (1)
      • = 1 + X + a⁵X²
    • Calculate l_μ+1=3=max(l_μ,l_p+μ-p)
      • = max(0,0+2-0)
      • = 2
    • Calculate d_μ+1=1 = S_μ+2 + σ₁^μ+1S_μ+1 ... + σ_lμ+1^μ+1 S_μ+2-lμ+1
      • Calculate the lowest S_i used to figure out when to stop
        • μ+2-l_μ+1 = 2+2-2=2, so the last S is S₂ = S_μ (since μ=2)
      • S_μ+2 + σ₁^μ+1S_μ+1 + σ₂^μ+1S_μ+2-2
        • = 1 + 1(a¹⁰) + a⁵(1)
        • = 1 + a¹⁰ + a⁵
        • = 1 + (1 + a + a²) + (a + a²)
        • = 0
  • Fill in the next row μ+1 = 3 with the calculated values

    μ	σμ(X)	dμ	lμ	μ-lμ
    -1	1	1	0	-1
    0	1	S1=1	0	0
    1	1 + X	0	1	0
    2	1 + X	a5	1	1
    3	1 + X + a5X2	0	2	1

  • μ = 3
    • d_μ=3 = 0, so next Newton identity satisfied
    • Set σ^μ+1(X) = σ^μ(X) = 1 + X + a⁵X²
    • Set l_μ+1 = l_μ = 2
    • Calculate d_μ+1=1 = S_μ+2 + σ₁^μ+1S_μ+1 ... + σ_lμ+1^μ+1 S_μ+2-lμ+1
      • Calculate the lowest S_i used to figure out when to stop
        • μ+2-l_μ+1 = 3+2-2=3, so the last S is S₃ = S_μ (since μ=3)
      • S_μ+2 + σ₁^μ+1S_μ+1 + σ₂^μ+1S_μ+2-2
        • = a¹⁰ + 1(1) + a⁵(a¹⁰)
        • = 1 + a + a² + 1 + a¹⁵
        • = 1 + a + a²
        • = a¹⁰
  • Fill in the next row μ+1 = 4 with the calculated values

    μ	σμ(X)	dμ	lμ	μ-lμ
    -1	1	1	0	-1
    0	1	S1=1	0	0
    1	1 + X	0	1	0
    2	1 + X	a5	1	1
    3	1 + X + a5X2	0	2	1
    4	1 + X + a5X2	a10	2	2

  • μ = 4
    • d_μ=4 = a¹⁰, not 0/next newton not satisfied
      • p = 2
    • Calculate σ^μ+1(X) = σ^μ(X) + d_μd_p^-1X^μ-p σ^p(X)
      • = σ⁴(X) + a¹⁰((a⁵)^-1)X² (1+X)
      • = (1 + X + a⁵X²) + (a¹⁰/a⁵)X²(1+X)
      • = (1 + X + a⁵X²) + (a^10-5)X²(1+X)
      • = 1 + X + a⁵X² + a⁵X² + a⁵X³
      • = 1 + X + a⁵X³
    • Calculate l_μ+1=5=max(l_μ,l_p+μ-p)
      • = max(2,1+4-2)
      • = 3
    • Calculate d_μ+1=1 = S_μ+2 + σ₁^μ+1S_μ+1 ... + σ_lμ+1^μ+1 S_μ+2-lμ+1
      • Calculate the lowest S_i used to figure out when to stop
        • μ+2-l_μ+1 = 4+2-3=3, so the last S is S₃, however S starts at 6 this time (μ+2) so there are 4 entries
      • S_μ+2 + σ₁^μ+1S_μ+1 + σ₂^μ+1S_μ+0 + σ₃^μ+1S_μ+2-3
        • = a⁵ + 1(a¹⁰) + 0(1) + a⁵a¹⁰
        • = a⁵ + a¹⁰ + a¹⁵
        • = a⁵ + a¹⁰ + 1
        • = a + a² + 1 + a + a² + 1
        • = 0
  • Fill in the next row μ+1 = 5 with the calculated values

    μ	σμ(X)	dμ	lμ	μ-lμ
    -1	1	1	0	-1
    0	1	S1=1	0	0
    1	1 + X	0	1	0
    2	1 + X	a5	1	1
    3	1 + X + a5X2	0	2	1
    4	1 + X + a5X2	a10	2	2
    5	1 + X + a5X3	0	3	2

  • μ = 5 = 2t-1 (last calculation)
    • d_μ=5 = 0, so σ^μ(X) satisfies the next Newton identity
    • Set σ^μ+1(X) = σ^μ(X)
      • = 1 + X + a⁵X³
      • This is our final result, the error location polynomial
  • Final resulting table

    μ	σμ(X)	dμ	lμ	μ-lμ
    -1	1	1	0	-1
    0	1	S1=1	0	0
    1	1 + X	0	1	0
    2	1 + X	a5	1	1
    3	1 + X + a5X2	0	2	1
    4	1 + X + a5X2	a10	2	2
    5	1 + X + a5X3	0	3	2
    6	1 + X + a5X3	-	-	-

• Calculate the roots of σ(X)
  • Chapter 2 literally suggests plugging in all power representations in the code for X and seeing which ones result in 0
    • σ(X) = 1 + X + a⁵X³
    • σ(0) = 1 + 0 + a⁵(0)³ = 1
    • σ(1) = 1 + 1 + a⁵(1)³ = a⁶
    • σ(a) = 1 + a + a⁵a³ = 1 + a + a⁸ = 1 + a + 1 + a² = a + a²
    • σ(a²) = 1 + a² + a⁵(a²)³ = 1 + a² + a¹¹ = 1 + a² + a + a² + a³ = 1 + a + a³
    • σ(a³) = 1 + a³ + a⁵(a³)³ = 1 + a³ + a¹⁴ = 1 + a³ + 1 + a³ = 0 (found a root!)
    • σ(a⁴) = 1 + a⁴ + a⁵(a⁴)³ = 1 + a⁴ + a¹⁷ = 1 + 1 + a + a² = a + a²
    • ...
  • Resulting roots for σ(X) = 0 are a³, a⁵, a¹²
• Take the inverses of te roots, whose powers are the error location numbers
  • (a³)^-1 = a^15-3 = a¹²
  • (a¹⁰)^-1 = a^15-10 = a⁵
  • (a¹²)^-1 = a^15-12 = a³
• Add the error locations to the received vector to get the final decoded word
  • r(X) + e(X) = (X³ + X⁵ + X¹²) + (X¹² + X⁵ + X³) = 0 = (0000000000000) = original codeword v(X)

Simplified Berlekamp Iterative Algorithm

• For binary BCH, the number of iterations can be reduced to t instead of 2t by only calculating even iterations
• Calculating the next row (μ+1) of the table is as follows:
  • If d_μ = 0, then σ^μ+1 = σ^μ(X)
  • Else pick previous row p where 2p-l_p is greatest and d_p =/= 0
    • Then calculate σ^μ+1(X) = σ^μ(X) + d_μd_p^-1X^2(μ-p)σ^p(X)
  • l_μ+1 = the degree of σ^μ+1
  • d_μ+1 = S_2μ+3 + σ₁^μ+1S_2μ+2 + σ₂^μ+1S_2μ+1 + ... σ_lμ+1^μ+1S_2μ+3-lμ+1
  • The difference value in the last column is 2μ-l_μ
• The starting table is

  μ	σμ(X)	dμ	lμ	2μ-lμ
  -1/2	1	1	0	-1
  0	1	S1	0	0
  1
  2
  ...
  t

• Additionally, the algorithm can terminate early if
  • Given μ, d_μ
  • For the next i=ceil((t-l_μ-1)/2) steps
  • If all d_i discrepancy values are 0, then σ^μ(X) is the next error location polynomial

Example of simplified Berlekamp Iterative Alg. for binary BCH

• Using same (15,5), t=3 BCH example above
• v,r are still the same
• The syndromes are still the same
• The starting table is now

  μ	σμ(X)	dμ	lμ	2μ-lμ
  -1/2	1	1	0	-1
  0	1	S1=1	0	0
  1
  2
  ...
  t

• μ = 0
  • d_{μ = 1, not zero, so find p}
  • p = -1/2 since only other row currently
  • σ^μ+1=1(X) = σ^μ=0(X) + d_μ=0d_p=-1/2^-1X^2(μ-p=1/2)σ^p=-1/2(X)
    • = 1 + 1(1^-1)X¹(1)
    • = 1 + X
  • l_μ+1 = degree(σ^μ+1(X)) = 1
  • d_μ+1 = S_2μ+3 + σ₁^μ+1S_2μ+2 + σ₂^μ+1S_2μ+1 + ... σ_lμ+1^μ+1S_2μ+3-lμ+1
    • Calculate last i used for S_i
      • = 2μ + 3 - l_μ+1
      • = 2(0) + 3 - 1
      • = 2
    • So d_μ+1 = S₃ + σ₁^μ+1S₂
      • = a¹⁰ + 1(1)
      • = 1 + a + a² + 1
      • = a⁵
• Fill in the table with our new data

  μ	σμ(X)	dμ	lμ	2μ-lμ
  -1/2	1	1	0	-1
  0	1	S1=1	0	0
  1	1 + X	a5	1	1
  2
  ...
  t

• μ = 1
  • d_{μ = a⁵, not zero, so find p}
  • p = 0 since largest 2μ-l_μ with non-zero discrepancy
  • σ^μ+1=2(X) = σ^μ=1(X) + d_μ=1d_p=0^-1X^2(μ-p=1)σ^p=0(X)
    • = (1 + X) + (a⁵)(1^-1)X²(1)
    • = 1 + X + a⁵X²
  • l_μ+1 = degree(σ^μ+1(X)) = 2
  • d_μ+1 = S_2μ+3 + σ₁^μ+1S_2μ+2 + σ₂^μ+1S_2μ+1 + ... σ_lμ+1^μ+1S_2μ+3-lμ+1
    • Calculate last i used for S_i
      • = 2μ + 3 - l_μ+1
      • = 2(1) + 3 - 2
      • = 3
    • So d_μ+1 = S₃
      • = a¹⁰
• Fill in the table with our new data

  μ	σμ(X)	dμ	lμ	2μ-lμ
  -1/2	1	1	0	-1
  0	1	S1=1	0	0
  1	1 + X	a5	1	1
  2	1 + X + a5X2	a10	2	2
  ...
  t

• μ = 2
  • d_{μ = a¹⁰, not zero, so find p}
  • p = 1 since largest 2μ-l_μ with non-zero discrepancy
  • σ^μ+1=3(X) = σ^μ=2(X) + d_μ=2d_p=1^-1X^2(μ-p=1)σ^p=1(X)
    • = (1 + X + a⁵X²) + a¹⁰(a⁵)^-1X²(1+X)
    • = 1 + X + a⁵X² + a^10-5X²(1 + X)
    • = 1 + X + a⁵X² + a⁵X²(1 + X)
    • = 1 + X + a⁵X² + a⁵X² + a⁵X³
    • = 1 + X + a⁵X³
  • l_μ+1 = degree(σ^μ+1(X)) = 3
  • End here since σ^μ+1=3(X) is the final error location polynomial, since t=3
• Fill in the table with our new data

  μ	σμ(X)	dμ	lμ	2μ-lμ
  -1/2	1	1	0	-1
  0	1	S1=1	0	0
  1	1 + X	a5	1	1
  2	1 + X + a5X2	a10	2	2
  3	1 + X + a5X3	-	-	-

• Finding roots of σ^μ=3(X) is the same as before, and our final error location polynomial is the same as before, so our final result is
  • e(X) + r(X) = (X³ + X⁵ + X¹²) + (X¹² + X⁵ + X³) = 0 = (0000000000000) = original codeword v(X)

Improved error location calculation (instead of 'finding roots of σ(X)')

• Given r(X), σ(X)
• For r_n-1, test if a^n-1 is an error location number
  • 1 + σ₁a + σ₂a² + ... + σ_va^v = 0
• σ₁a,σ₂a², ... are pre calculated
• If sum is not zero then r_n-1 not an error digit
• Circuit for this given in figure 6.1